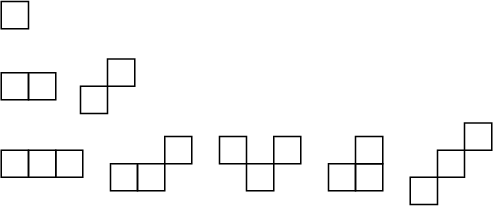
|
|
|
A Polyomino-like object made by attaching squares joined either at sides or corners. Because neighboring squares can be
in relation to one another as Kings may move on a Chessboard, polyplets are sometimes also
called Polykings. The number of 
-polyplets (with holes allowed) are 1, 2, 5, 22, 94, 524, 3031, ...
(Sloane's A030222). The number of -polyplets having bilateral symmetry are 1, 2, 4, 10, 22, 57, 131, ... (Sloane's A030234).
The number of -polyplets not having bilateral symmetry are 0, 0, 1, 12, 72, 467, 2900, ... (Sloane's A030235). The number
of fixed -polyplets are 1, 4, 20, 110, 638, 3832, ... (Sloane's A030232). The number of one-sided -polyplets are 1, 2,
6, 34, 166, 991, ... (Sloane's A030233).
See also Polyiamond, Polyomino
References
Sloane, N. J. A. Sequences
A030222,
A030232,
A030233,
A030234, and
A030235
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.