|
|
|
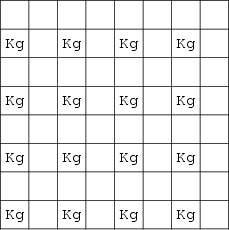
The problem of determining how many nonattacking kings can be placed on an ![]() Chessboard. For
Chessboard. For ![]() , the
solution is 16, as illustrated above (Madachy 1979). In general, the solutions are
, the
solution is 16, as illustrated above (Madachy 1979). In general, the solutions are
| (1) |
| (2) |
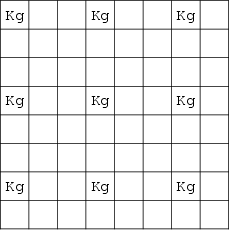
The minimum number of kings needed to attack or occupy all squares on an ![]() Chessboard is nine, illustrated above
(Madachy 1979).
Chessboard is nine, illustrated above
(Madachy 1979).
See also Bishops Problem, Chess, Hard Hexagon Entropy Constant, Knights Problem, Queens Problem, Rooks Problem
References
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 39, 1979.