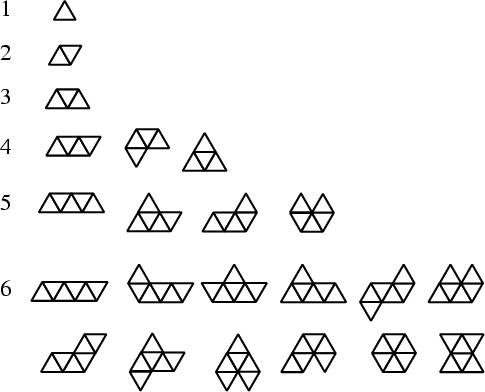
|
|
|
A generalization of the Polyominoes using a collection of equal-sized Equilateral Triangles (instead of Squares) arranged with coincident sides. Polyiamonds are sometimes simply known as Iamonds.
The number of two-sided (i.e., can be picked up and flipped, so Mirror Image pieces are considered identical)
polyiamonds made up of 
triangles are 1, 1, 1, 3, 4, 12, 24, 66, 160, 448, ... (Sloane's A000577). The number of
one-sided polyiamonds composed of triangles are 1, 1, 1, 4, 6, 19, 43, 121, ... (Sloane's A006534). No
Holes are possible with fewer than seven triangles.
The top row of 6-polyiamonds in the above figure are known as the Bar, Crook, Crown, Sphinx, Snake, and Yacht. The bottom row of 6-polyiamonds are known as the Chevron, Signpost, Lobster, Hook, Hexagon, and Butterfly.
See also Polyabolo, Polyhex, Polyomino
References
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Gardner, M. ``Mathematical Games.'' Sci. Amer., Dec. 1964.
Golomb, S. W. Polyominoes: Puzzles, Patterns, Problems, and Packings, 2nd ed.
Princeton, NJ: Princeton University Press, pp. 90-92, 1994.
Sloane, N. J. A. Sequences
A000577/M2374
and A006534/M3287
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
von Seggern, D. CRC Standard Curves and Surfaces. Boca Raton, FL: CRC Press, pp. 342-343, 1993.