If the Coefficients of the Polynomial
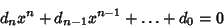 |
(1) |
are specified to be Integers, then integral Roots must have a Numerator which is a
factor of 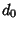 and a Denominator which is a factor of
and a Denominator which is a factor of 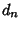 (with either sign possible). This follows since a
Polynomial of Order
(with either sign possible). This follows since a
Polynomial of Order 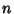 with
with 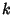 integral Roots can be expressed as
integral Roots can be expressed as
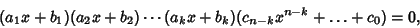 |
(2) |
where the Roots are
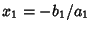 ,
,
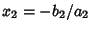 , ..., and
, ..., and
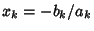 . Factoring out the
. Factoring out the
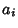 s,
s,
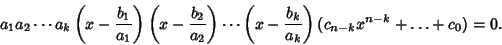 |
(3) |
Now, multiplying through,
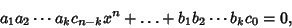 |
(4) |
where we have not bothered with the other terms. Since the first and last Coefficients are 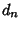 and
and
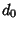 , all the integral roots of (1) are of the form [factors of
, all the integral roots of (1) are of the form [factors of 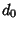 ]/[factors of
]/[factors of 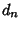 ].
].
© 1996-9 Eric W. Weisstein
1999-05-25