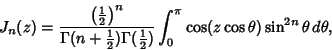A.k.a. Bessel's Second Integral.
where 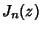 is a Bessel Function of the First Kind and
is a Bessel Function of the First Kind and 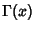 is a Gamma Function. It can be derived
from Sonine's Integral. With
is a Gamma Function. It can be derived
from Sonine's Integral. With 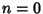 , the integral becomes Parseval's Integral.
, the integral becomes Parseval's Integral.
See also Bessel Function of the First Kind, Parseval's Integral, Sonine's Integral
© 1996-9 Eric W. Weisstein
1999-05-25