|
|
|
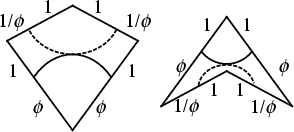
A pair of shapes which tile the plane only aperiodically (when the markings are constrained to match at borders). The two tiles, illustrated above, are called the ``Kite'' and ``Dart.''
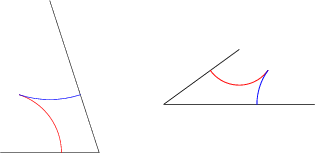
To see how the plane may be tiled aperiodically using the kite and dart, divide the kite into acute and obtuse tiles, shown above. Now define ``deflation'' and ``inflation'' operations. The deflation operator takes an acute Triangle to the union of two Acute Triangles and one Obtuse, and the Obtuse Triangle goes to an Acute and an Obtuse Triangle. These operations are illustrated below.
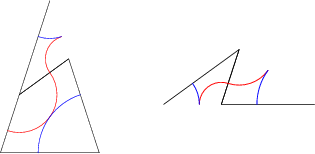
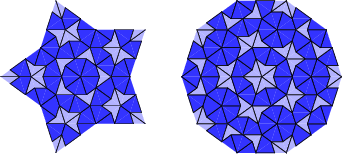
When applied to a collection of tiles, the deflation operator leads to a more refined collection. The operators do not respect tile boundaries, but do respect the half tiles defined above. There are two ways to obtain aperiodic Tilings with 5-fold symmetry about a single point. They are known an the ``star'' and ``sun'' configurations, and are show below.
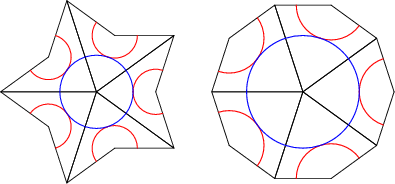
Higher order versions can then be obtained by deflation. For example, the following are third-order deflations:
References
Gardner, M. Chs. 1-2 in Penrose Tiles and Trapdoor Ciphers... and the Return of Dr. Matrix, reissue ed. New York: W. H. Freeman, pp. 299-300, 1989.
Peterson, I. The Mathematical Tourist: Snapshots of Modern Mathematics. New York: W. H. Freeman, pp. 86-95, 1988.
Wagon, S. ``Penrose Tiles.'' §4.3 in Mathematica in Action. New York: W. H. Freeman, pp. 108-117, 1991.
![]() Hurd, L. P. ``PenroseTiles.''
http://www.mathsource.com/cgi-bin/MathSource/Applications/Graphics/2D/0206-772.
Hurd, L. P. ``PenroseTiles.''
http://www.mathsource.com/cgi-bin/MathSource/Applications/Graphics/2D/0206-772.