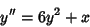Painlevé Transcendents

$$y''=6y^2+x$$ (1)

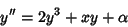$$y''=2y^3+xy+\alpha$$ (2)

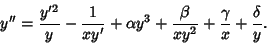$$y''={y'^2\over y}-{1\over xy'}+\alpha y^3+{\beta\over xy^2}+{\gamma\over x}+{\delta\over y}.$$ (3)

Transcendents 4-6 do not have known first integrals, but all transcendents have first integrals for special values of their parameters except (1). Painlevé found the above transcendents (1) to (3), and the rest were investigated by his students. The sixth transcendent was found by Gambier and contains the other five as limiting cases.

See also Painlevé Property