Following the work of Fuchs in classifying first-order Ordinary Differential Equations, Painlevé studied second-order ODEs of the form
where 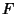 is Analytic in
is Analytic in 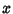 and rational in
and rational in 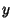 and
and 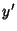 . Painlevé
. Painlevé  found 50 types whose only movable Singularities are ordinary Poles. This characteristic
is known as the Painlevé property. Six of the transcendents define new transcendents known as Painlevé
Transcendents, and the remaining 44 can be integrated in terms of classical transcendents,
quadratures, or the Painlevé Transcendents.
found 50 types whose only movable Singularities are ordinary Poles. This characteristic
is known as the Painlevé property. Six of the transcendents define new transcendents known as Painlevé
Transcendents, and the remaining 44 can be integrated in terms of classical transcendents,
quadratures, or the Painlevé Transcendents.
See also Painlevé Transcendents
© 1996-9 Eric W. Weisstein
1999-05-26