Consider a first-order ODE in the slightly different form
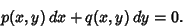 |
(1) |
Such an equation is said to be exact if
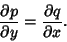 |
(2) |
This statement is equivalent to the requirement that a Conservative Field exists, so that a scalar potential can be
defined. For an exact equation, the solution is
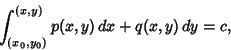 |
(3) |
where 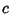 is a constant.
is a constant.
A first-order ODE (1) is said to be inexact if
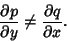 |
(4) |
For a nonexact equation, the solution may be obtained by defining an Integrating Factor 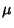 of (6) so that the
new equation
of (6) so that the
new equation
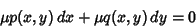 |
(5) |
satisfies
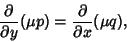 |
(6) |
or, written out explicitly,
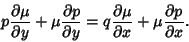 |
(7) |
This transforms the nonexact equation into an exact one. Solving (7) for 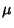 gives
gives
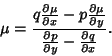 |
(8) |
Therefore, if a function 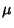 satisfying (8) can be found, then writing
satisfying (8) can be found, then writing
in equation (5) then gives
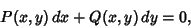 |
(11) |
which is then an exact ODE. Special cases in which 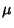 can be found include
can be found include 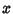 -dependent,
-dependent, 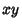 -dependent, and
-dependent, and
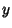 -dependent integrating factors.
-dependent integrating factors.
Given an inexact first-order ODE, we can also look for an Integrating Factor 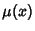 so that
so that
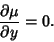 |
(12) |
For the equation to be exact in 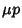 and
and 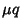 , the equation for a first-order nonexact ODE
, the equation for a first-order nonexact ODE
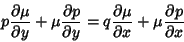 |
(13) |
becomes
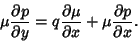 |
(14) |
Solving for
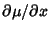 gives
gives
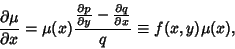 |
(15) |
which will be integrable if
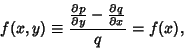 |
(16) |
in which case
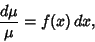 |
(17) |
so that the equation is integrable
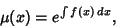 |
(18) |
and the equation
![\begin{displaymath}[\mu p(x,y)]dx+[\mu q(x,y)]dy = 0
\end{displaymath}](o_681.gif) |
(19) |
with known 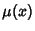 is now exact and can be solved as an exact ODE.
is now exact and can be solved as an exact ODE.
Given in an exact first-order ODE, look for an Integrating Factor
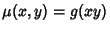 . Then
. Then
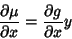 |
(20) |
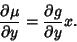 |
(21) |
Combining these two,
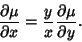 |
(22) |
For the equation to be exact in 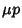 and
and 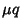 , the equation for a first-order nonexact ODE
, the equation for a first-order nonexact ODE
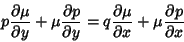 |
(23) |
becomes
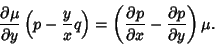 |
(24) |
Therefore,
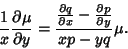 |
(25) |
Define a new variable
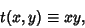 |
(26) |
then
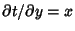 , so
, so
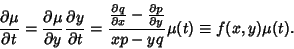 |
(27) |
Now, if
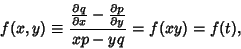 |
(28) |
then
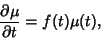 |
(29) |
so that
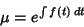 |
(30) |
and the equation
![\begin{displaymath}[\mu p(x,y)]\,dx+[\mu q(x,y)]\,dy = 0
\end{displaymath}](o_694.gif) |
(31) |
is now exact and can be solved as an exact ODE.
Given an inexact first-order ODE, assume there exists an integrating factor
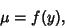 |
(32) |
so
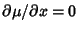 . For the equation to be exact in
. For the equation to be exact in 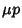 and
and 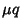 , equation (7) becomes
, equation (7) becomes
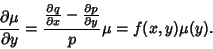 |
(33) |
Now, if
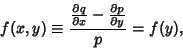 |
(34) |
then
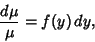 |
(35) |
so that
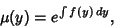 |
(36) |
and the equation
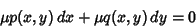 |
(37) |
is now exact and can be solved as an exact ODE.
Given a first-order ODE of the form
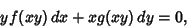 |
(38) |
define
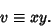 |
(39) |
Then the solution is
![\begin{displaymath}
\cases{
\ln x = \int{g(v)\,dv\over c[g(v)-f(v)]} + c & for $g(v) \not = f(v)$\cr
xy = c & for $g(v) = f(v)$.\cr}
\end{displaymath}](o_702.gif) |
(40) |
If
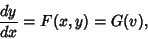 |
(41) |
where
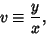 |
(42) |
then letting
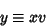 |
(43) |
gives
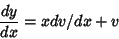 |
(44) |
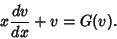 |
(45) |
This can be integrated by quadratures, so
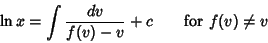 |
(46) |
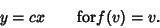 |
(47) |
References
Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed.
New York: Wiley, 1986.
© 1996-9 Eric W. Weisstein
1999-05-26
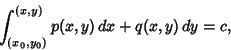
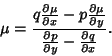
![]() so that
so that
![]() . Then
. Then