The following conditions are equivalent for a conservative Vector Field:
- 1. For any oriented simple closed curve
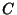 , the Line Integral
, the Line Integral
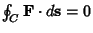 .
.
- 2. For any two oriented simple curves
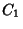 and
and 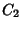 with the same endpoints,
with the same endpoints,
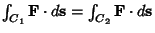 .
.
- 3. There exists a Scalar Potential Function
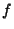 such that
such that
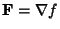 , where
, where  is the
Gradient.
is the
Gradient.
- 4. The Curl
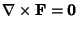 .
.
See also Curl, Gradient, Line Integral, Potential Function, Vector Field
© 1996-9 Eric W. Weisstein
1999-05-26