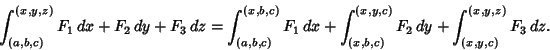The line integral on a curve
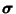 is defined by
is defined by
where
![\begin{displaymath}
{\bf F} \equiv \left[{\matrix{F_1\cr F_2\cr F_3\cr}}\right].
\end{displaymath}](l2_238.gif) |
(3) |
If
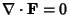 (i.e., it is a Divergenceless Field), then the line integral is path independent and
(i.e., it is a Divergenceless Field), then the line integral is path independent and
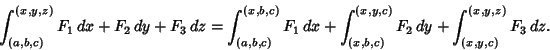 |
(4) |
For 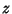 Complex,
Complex,
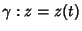 , and
, and ![$t\in[a,b]$](l2_243.gif) ,
,
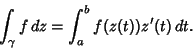 |
(5) |
See also Contour Integral, Path Integral
© 1996-9 Eric W. Weisstein
1999-05-25
![]() is defined by
is defined by
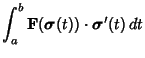
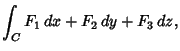
![\begin{displaymath}
{\bf F} \equiv \left[{\matrix{F_1\cr F_2\cr F_3\cr}}\right].
\end{displaymath}](l2_238.gif)