|
|
|
Let ![]() be a Path given parametrically by
be a Path given parametrically by
![]() . Let
. Let ![]() denote Arc Length from the initial
point. Then
denote Arc Length from the initial
point. Then
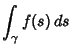 |
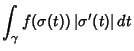 |
||
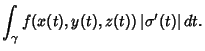 |
See also Line Integral
References
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Evaluation of Functions by Path Integration.'' §5.14 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 201-204, 1992.