Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/onenin/onenin.html
Carpenter, A. J.; Ruttan, A.; and Varga, R. S. ``Extended Numerical Computations on the `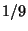 ' Conjecture in Rational Approximation Theory.''
In Rational approximation and interpolation (Tampa, Fla., 1983) (Ed. P. R. Graves-Morris, E. B. Saff, and R. S. Varga).
New York: Springer-Verlag, pp. 383-411, 1984.
' Conjecture in Rational Approximation Theory.''
In Rational approximation and interpolation (Tampa, Fla., 1983) (Ed. P. R. Graves-Morris, E. B. Saff, and R. S. Varga).
New York: Springer-Verlag, pp. 383-411, 1984.
Cody, W. J.; Meinardus, G.; and Varga, R. S. ``Chebyshev Rational Approximations to 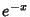 in
in 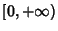 and Applications to
Heat-Conduction Problems.'' J. Approx. Th. 2, 50-65, 1969.
and Applications to
Heat-Conduction Problems.'' J. Approx. Th. 2, 50-65, 1969.
Dunham, C. B. and Taylor, G. D. ``Continuity of Best Reciprocal Polynomial Approximation on 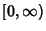 .''
J. Approx. Th. 30, 71-79, 1980.
.''
J. Approx. Th. 30, 71-79, 1980.
Gonchar, A. A. ``Rational Approximations of Analytic Functions.'' Amer. Math. Soc. Transl. Ser. 2 147, 25-34, 1990.
Gonchar, A. A. and Rakhmanov, E. A. ``Equilibrium Distributions and Degree of Rational Approximation of Analytic
Functions.'' Math. USSR Sbornik 62, 305-348, 1980.
Magnus, A. P. ``On Freud's Equations for Exponential Weights, Papers Dedicated to the Memory of Géza Freud.''
J. Approx. Th. 46, 65-99, 1986.
Rahman, Q. I. and Schmeisser, G. ``Rational Approximation to the Exponential Function.'' In Padé and Rational Approximation,
(Proc. Internat. Sympos., Univ. South Florida, Tampa, Fla., 1976) (Ed. E. B. Saff and R. S. Varga).
New York: Academic Press, pp. 189-194, 1977.
Schönhage, A. ``Zur rationalen Approximierbarkeit von 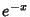 über
über 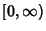 .'' J. Approx. Th. 7, 395-398, 1973.
.'' J. Approx. Th. 7, 395-398, 1973.
Varga, R. S. Scientific Computations on Mathematical Problems and Conjectures. Philadelphia, PA: SIAM, 1990.
![]() be Chebyshev Constants. Schönhage (1973) proved that
be Chebyshev Constants. Schönhage (1973) proved that
![\begin{displaymath}
\Lambda=\mathop{\rm exp}\nolimits \left[{-{\pi K(\sqrt{1-c^2}\,)\over K(c)}}\right],
\end{displaymath}](o_385.gif)
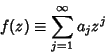
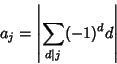
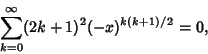
![]() ' Conjecture in Rational Approximation Theory.''
In Rational approximation and interpolation (Tampa, Fla., 1983) (Ed. P. R. Graves-Morris, E. B. Saff, and R. S. Varga).
New York: Springer-Verlag, pp. 383-411, 1984.
' Conjecture in Rational Approximation Theory.''
In Rational approximation and interpolation (Tampa, Fla., 1983) (Ed. P. R. Graves-Morris, E. B. Saff, and R. S. Varga).
New York: Springer-Verlag, pp. 383-411, 1984.
![]() in
in ![]() and Applications to
Heat-Conduction Problems.'' J. Approx. Th. 2, 50-65, 1969.
and Applications to
Heat-Conduction Problems.'' J. Approx. Th. 2, 50-65, 1969.
![]() .''
J. Approx. Th. 30, 71-79, 1980.
.''
J. Approx. Th. 30, 71-79, 1980.
![]() über
über ![]() .'' J. Approx. Th. 7, 395-398, 1973.
.'' J. Approx. Th. 7, 395-398, 1973.