|
|
|
A Root-finding Algorithm which uses the first few terms of the Taylor Series in the vicinity of a
suspected Root to zero in on the root. The Taylor Series of a function ![]() about the point
about the point ![]() is
given by
is
given by
| (1) |
| (2) |
| (3) |
Unfortunately, this procedure can be unstable near a horizontal Asymptote or a Local Minimum. However, with a
good initial choice of the Root's position, the algorithm can by applied iteratively to obtain
| (4) |
The error
![]() after the
after the ![]() st iteration is given by
st iteration is given by
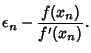 |
(5) |
| (6) | |||
| (7) |
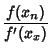 |
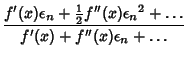 |
||
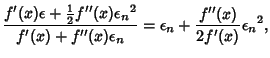 |
(8) |
| (9) |
A Fractal is obtained by applying Newton's method to finding a Root of ![]() (Mandelbrot 1983, Gleick 1988,
Peitgen and Saupe 1988, Press et al. 1992, Dickau 1997). Iterating for a starting point
(Mandelbrot 1983, Gleick 1988,
Peitgen and Saupe 1988, Press et al. 1992, Dickau 1997). Iterating for a starting point ![]() gives
gives
| (10) |

Coloring the Basin of Attraction (the set of initial points ![]() which converge to the same Root) for
each Root a different color then gives the above plots, corresponding to
which converge to the same Root) for
each Root a different color then gives the above plots, corresponding to ![]() , 3, 4, and 5.
, 3, 4, and 5.
See also Halley's Irrational Formula, Halley's Method, Householder's Method, Laguerre's Method
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 18, 1972.
Acton, F. S. Ch. 2 in Numerical Methods That Work. Washington, DC: Math. Assoc. Amer., 1990.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 963-964, 1985.
Dickau, R. M. ``Basins of Attraction for
Dickau, R. M. ``Variations on Newton's Method.''
http://forum.swarthmore.edu/advanced/robertd/newnewton.html.
Dickau, R. M. ``Compilation of Iterative and List Operations.'' Mathematica J. 7, 14-15, 1997.
Gleick, J. Chaos: Making a New Science. New York: Penguin Books, plate 6 (following pp. 114) and p. 220, 1988.
Householder, A. S. Principles of Numerical Analysis.ew York: McGraw-Hill, pp. 135-138, 1953.
Mandelbrot, B. B. The Fractal Geometry of Nature. San Francisco, CA: W. H. Freeman, 1983.
Ortega, J. M. and Rheinboldt, W. C. Iterative Solution of Nonlinear Equations in Several Variables.
New York: Academic Press, 1970.
Peitgen, H.-O. and Saupe, D. The Science of Fractal Images. New York: Springer-Verlag, 1988.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Newton-Raphson Method Using Derivatives''
and ``Newton-Raphson Methods for Nonlinear Systems of Equations.'' §9.4 and 9.6 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed.
Cambridge, England: Cambridge University Press, pp. 355-362 and 372-375, 1992.
Ralston, A. and Rabinowitz, P. §8.4 in A First Course in Numerical Analysis, 2nd ed. New York: McGraw-Hill,
1978.
![]() Using Newton's Method in the Complex Plane.''
http://forum.swarthmore.edu/advanced/robertd/newtons.html.
Using Newton's Method in the Complex Plane.''
http://forum.swarthmore.edu/advanced/robertd/newtons.html.
|
|
|
© 1996-9 Eric W. Weisstein