An algorithm for the Square Root of a number 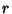 quadratically as
quadratically as
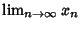 ,
,
where 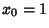 . The first few approximants to
. The first few approximants to 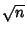 are given by
are given by
For 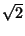 , this gives the convergents as 1, 3/2, 17/12, 577/408, 665857/470832, ....
, this gives the convergents as 1, 3/2, 17/12, 577/408, 665857/470832, ....
See also Square Root
© 1996-9 Eric W. Weisstein
1999-05-25
![]() quadratically as
quadratically as
![]() ,
,