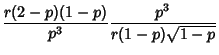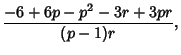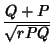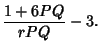Also known as the Pascal Distribution and Pólya Distribution. The probability of
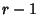 successes and
successes and 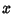 failures in
failures in 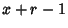 trials, and success on the
trials, and success on the 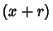 th trial is
th trial is
![\begin{displaymath}
p\left[{{x+r-1\choose r-1} p^{r-1}(1-p)^{[(x+r-1)-(r-1)]}}\r...
...se r-1}p^{r-1}(1-p)^x}\right]p = {x+r-1\choose r-1}p^r(1-p)^x,
\end{displaymath}](n_186.gif) |
(1) |
where 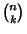 is a Binomial Coefficient. Let
is a Binomial Coefficient. Let
The Characteristic Function is given by
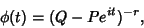 |
(4) |
and the Moment-Generating Function by
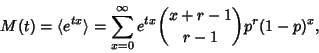 |
(5) |
but, since
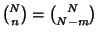 ,
,
The Moments about zero
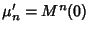 are therefore
are therefore
(Beyer 1987, p. 487, apparently gives the Mean incorrectly.)
The Moments about the mean are
The Mean, Variance, Skewness and Kurtosis are then
which can also be written
The first Cumulant is
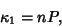 |
(24) |
and subsequent Cumulants are given by the recurrence relation
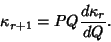 |
(25) |
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 533, 1987.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, p. 118, 1992.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() successes and
successes and ![]() failures in
failures in ![]() trials, and success on the
trials, and success on the ![]() th trial is
th trial is
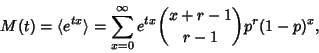
![$\displaystyle p^r \sum_{x=0}^\infty{x+r-1\choose x}[(1-p)e^t]^x$](n_196.gif)
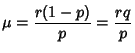
![$\displaystyle {r(1-p)[1-r(p-1)]\over p^2}={rq(1-rq)\over p^2}$](n_209.gif)
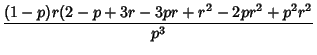
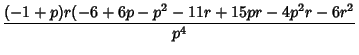
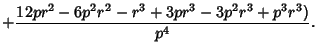
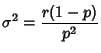
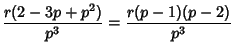
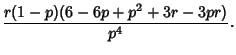
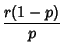
![$\displaystyle {\mu_3\over\sigma^3}={r(p-1)(p-2)\over p^3} \left[{p^2\over r(1-p)}\right]^{3/2}$](n_225.gif)