Let 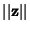 be a Vector Norm of
be a Vector Norm of 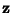 such that
such that
Then
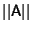 is a Matrix Norm which is said to be the natural norm Induced (or
Subordinate) to the Vector Norm
is a Matrix Norm which is said to be the natural norm Induced (or
Subordinate) to the Vector Norm 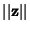 . For any natural norm,
. For any natural norm,
where
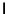 is the Identity Matrix. The natural matrix norms induced by the L1-Norm,
L2-Norm, and L(infinity)-Norm are called the Maximum
Absolute Column Sum Norm, Spectral Norm, and Maximum Absolute Row Sum Norm, respectively.
is the Identity Matrix. The natural matrix norms induced by the L1-Norm,
L2-Norm, and L(infinity)-Norm are called the Maximum
Absolute Column Sum Norm, Spectral Norm, and Maximum Absolute Row Sum Norm, respectively.
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, p. 1115, 1979.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() be a Vector Norm of
be a Vector Norm of ![]() such that
such that