|
|
|
A Vector Norm defined for a Vector
![\begin{displaymath}
{\bf x} = \left[{\matrix{x_1\cr x_2\cr \vdots\cr x_n\cr}}\right],
\end{displaymath}](l1_1.gif)
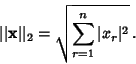
See also L1-Norm, L2-Space, L(infinity)-Norm, Parallelogram Law, Vector Norm
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, pp. 1114-1125, 1979.