Malfatti's Tangent Triangle Problem

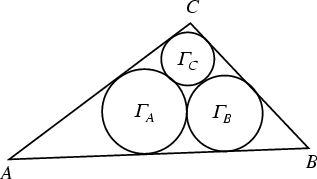
Draw within a given Triangle three Circles, each of which is Tangent to the other two and to two sides of the Triangle. Denote the three Circles so constructed $\Gamma_A$, $\Gamma_B$, and $\Gamma_C$. Then $\Gamma_A$ is tangent to $AB$ and $AC$, $\Gamma_B$ is tangent to $BC$ and $BA$, and $\Gamma_C$ is tangent to $AC$ and $BC$.

See also Ajima-Malfatti Points, Malfatti's Right Triangle Problem

References

Dörrie, H. ``Malfatti's Problem.'' §30 in 100 Great Problems of Elementary Mathematics: Their History and Solutions. New York: Dover, pp. 147-151, 1965.

Forder, H. G. Higher Course Geometry. Cambridge, England: Cambridge University Press, pp. 244-245, 1931.

Fukagawa, H. and Pedoe, D. Japanese Temple Geometry Problems (San Gaku). Winnipeg: The Charles Babbage Research Centre, pp. 106-120, 1989.

Gardner, M. Fractal Music, Hypercards, and More Mathematical Recreations from Scientific American Magazine. New York: W. H. Freeman, pp. 163-165, 1992.

Goldberg, M. ``On the Original Malfatti Problem.'' Math. Mag. 40, 241-247, 1967.

Lob, H. and Richmond, H. W. ``On the Solution of Malfatti's Problem for a Triangle.'' Proc. London Math. Soc. 2, 287-304, 1930.

Woods, F. S. Higher Geometry. New York: Dover, pp. 206-209, 1961.