|
|
|
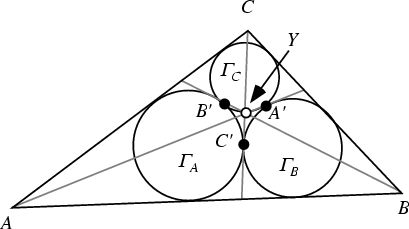
The lines connecting the vertices and corresponding circle-circle intersections in Malfatti's Tangent Triangle
Problem coincide in a point ![]() called the first Ajima-Malfatti point (Kimberling and MacDonald 1990, Kimberling 1994).
Similarly, letting
called the first Ajima-Malfatti point (Kimberling and MacDonald 1990, Kimberling 1994).
Similarly, letting ![]() ,
, ![]() , and
, and ![]() be the excenters of
be the excenters of ![]() , then the lines
, then the lines ![]() ,
, ![]() , and
, and ![]() are coincident in another point called the second Ajima-Malfatti point. The points are sometimes simply called the
Malfatti Points (Kimberling 1994).
are coincident in another point called the second Ajima-Malfatti point. The points are sometimes simply called the
Malfatti Points (Kimberling 1994).
References
Kimberling, C. ``Central Points and Central Lines in the Plane of a Triangle.'' Math. Mag. 67,
163-187, 1994.
Kimberling, C. ``1st and 2nd Ajima-Malfatti Points.''
http://cedar.evansville.edu/~ck6/tcenters/recent/ajmalf.html.
Kimberling, C. and MacDonald, I. G. ``Problem E 3251 and Solution. '' Amer. Math. Monthly 97, 612-613, 1990.