|
|
|
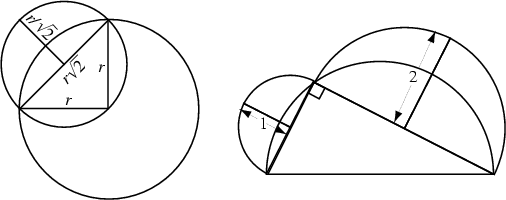
A figure bounded by two circular Arcs of unequal Radii. Hippocrates of Chios
Squared the above left lune, as well as two others, in the fifth century BC. ![]() Two more
Squarable lunes were found by T. Clausen in the 19th century (Dunham 1990 attributes these discoveries to Euler
Two more
Squarable lunes were found by T. Clausen in the 19th century (Dunham 1990 attributes these discoveries to Euler ![]() in 1771). In the 20th century, N. G. Tschebatorew and A. W. Dorodnow proved that these are the only five squarable lunes
(Shenitzer and Steprans 1994). The left lune above is squared as follows,
in 1771). In the 20th century, N. G. Tschebatorew and A. W. Dorodnow proved that these are the only five squarable lunes
(Shenitzer and Steprans 1994). The left lune above is squared as follows,
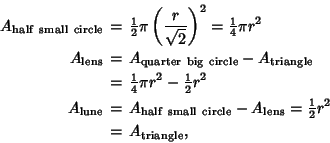
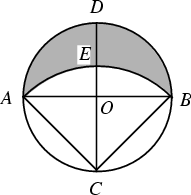
For the above lune,
See also Annulus, Arc, Circle, Lune (Surface)
References
Dunham, W. ``Hippocrates' Quadrature of the Lune.'' Ch. 1 in
Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 1-20, 1990.
Heath, T. L. A History of Greek Mathematics, Vol. 1: From Thales to Euclid. New York: Dover, p. 185, 1981.
Pappas, T. ``Lunes.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 72-73, 1989.
Shenitzer, A. and Steprans, J. ``The Evolution of Integration.'' Amer. Math. Monthly 101, 66-72, 1994.