|
|
|
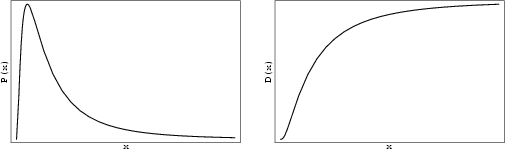
A Continuous Distribution in which the Logarithm of a variable has a Normal Distribution.
It is a general case of Gilbrat's Distribution, to which the log normal distribution reduces with ![]() and
and
![]() . The probability density and cumulative distribution functions for the log normal distribution are
. The probability density and cumulative distribution functions for the log normal distribution are
| (1) | |||
![$\displaystyle {1\over 2}\left[{1+\mathop{\rm erf}\nolimits \left({\ln x-M\over S\sqrt{2}}\right)}\right],$](l2_548.gif) |
(2) |
| (3) |
| (4) | |||
| (5) | |||
| (6) | |||
| (7) |
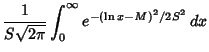 |
|||
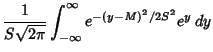 |
|||
![$\displaystyle {1\over S\sqrt{2\pi}} \int_{-\infty}^\infty e^{-[-y+(y-M)^2/2S^2]}\,dy$](l2_564.gif) |
|||
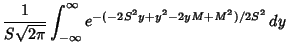 |
|||
![$\displaystyle {1\over S\sqrt{2\pi}} \int_{-\infty}^\infty e^{-\{[y-(S^2+M)]^2+S^2(S^2+2M)\}/2S^2}\,dy$](l2_566.gif) |
|||
![$\displaystyle {1\over S\sqrt{2\pi}} e^{M+S^2/2} \int_{-\infty}^\infty e^{-[y-(S^2+M)]^2/2S^2}\,dy$](l2_567.gif) |
|||
| (8) |
See also Gilbrat's Distribution, Weibull Distribution
References
Aitchison, J. and Brown, J. A. C. The Lognormal Distribution, with Special Reference to Its Use in Economics.
New York: Cambridge University Press, 1957.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand,
p. 123, 1951.
|
|
|
© 1996-9 Eric W. Weisstein