|
|
|
States that for a nondissipative Hamiltonian System, phase space density (the Area between phase space
contours) is constant. This requires that, given a small time increment ![]() ,
,
| (1) |
| (2) |
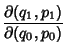 |
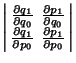 |
||
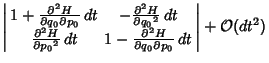 |
|||
| (3) |
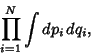 |
(4) |
See also Liouville Measure, Phase Space
References
Chavel, I. Riemannian Geometry: A Modern Introduction. New York: Cambridge University
Press, 1994.