|
|
|
Given a Map ![]() from a Space
from a Space ![]() to a Space
to a Space ![]() and another Map
and another Map ![]() from a Space
from a Space ![]() to a Space
to a Space ![]() , a lift is a Map
, a lift is a Map ![]() from
from ![]() to
to ![]() such that
such that ![]() . In other words, a lift of
. In other words, a lift of ![]() is
a Map
is
a Map ![]() such that the diagram (shown below) commutes.
such that the diagram (shown below) commutes.
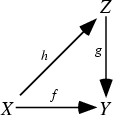
If ![]() is the identity from
is the identity from ![]() to
to ![]() , a Manifold, and if
, a Manifold, and if ![]() is the bundle projection from the Tangent Bundle to
is the bundle projection from the Tangent Bundle to
![]() , the lifts are precisely Vector Fields. If
, the lifts are precisely Vector Fields. If ![]() is a bundle projection from any Fiber Bundle
to
is a bundle projection from any Fiber Bundle
to ![]() , then lifts are precisely sections. If
, then lifts are precisely sections. If ![]() is the identity from
is the identity from ![]() to
to ![]() , a Manifold, and
, a Manifold, and ![]() a projection from
the orientation double cover of
a projection from
the orientation double cover of ![]() , then lifts exist Iff
, then lifts exist Iff ![]() is an orientable Manifold.
is an orientable Manifold.
If ![]() is a Map from a Circle to
is a Map from a Circle to ![]() , an
, an ![]() -Manifold, and
-Manifold, and ![]() the bundle projection from the Fiber
Bundle of alternating k-Form on
the bundle projection from the Fiber
Bundle of alternating k-Form on ![]() , then lifts always exist Iff
, then lifts always exist Iff ![]() is orientable. If
is orientable. If ![]() is a
Map from a region in the Complex Plane to the Complex Plane (complex analytic), and if
is a
Map from a region in the Complex Plane to the Complex Plane (complex analytic), and if ![]() is the
exponential Map, lifts of
is the
exponential Map, lifts of ![]() are precisely Logarithms of
are precisely Logarithms of ![]() .
.
See also Lifting Problem