where 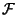 is the Fourier Transform of the probability
is the Fourier Transform of the probability 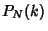 for
for 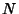 -step addition of random variables.
Lévy showed that
-step addition of random variables.
Lévy showed that 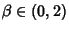 for
for 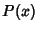 to be Nonnegative. The Lévy distribution has infinite variance
and sometimes infinite mean. The case
to be Nonnegative. The Lévy distribution has infinite variance
and sometimes infinite mean. The case 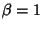 gives a Cauchy Distribution, while
gives a Cauchy Distribution, while 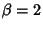 gives a
Gaussian Distribution.
gives a
Gaussian Distribution.
See also Cauchy Distribution, Gaussian Distribution
© 1996-9 Eric W. Weisstein
1999-05-26