|
|
|
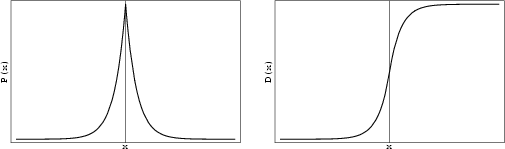
Also called the Double Exponential Distribution. It is the distribution of differences between two independent
variates with identical Exponential Distributions (Abramowitz and Stegun 1972,
p. 930).
| (1) | |||
| (2) |
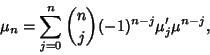 |
(3) |
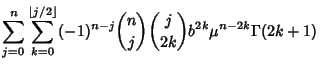 |
|||
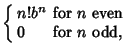 |
(4) |
The Moments can also be computed using the Characteristic Function,
| (5) |
| (6) |
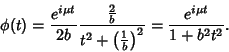 |
(7) |
| (8) |
| (9) | |||
| (10) | |||
| (11) | |||
| (12) |
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, 1972.
|
|
|
© 1996-9 Eric W. Weisstein