|
|
|
Also known as Metric Entropy. Divide Phase Space into ![]() -dimensional Hypercubes of
Content
-dimensional Hypercubes of
Content ![]() . Let
. Let
![]() be the probability that a trajectory is in Hypercube
be the probability that a trajectory is in Hypercube ![]() at
at ![]() ,
, ![]() at
at ![]() ,
, ![]() at
at ![]() , etc. Then define
, etc. Then define
| (1) |
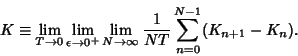 |
(2) |
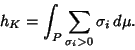 |
(3) |
See also Hypercube, Lyapunov Characteristic Exponent
References
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, p. 138, 1993.
Schuster, H. G. Deterministic Chaos: An Introduction, 3rd ed. New York: Wiley, p. 112, 1995.