|
|
|
The Lyapunov characteristic exponent [LCE] gives the rate of exponential divergence from perturbed initial conditions. To examine
the behavior of an orbit around a point ![]() , perturb the system and write
, perturb the system and write
| (1) |
| (2) |
| (3) |
One Lyapunov characteristic exponent is always 0, since there is never any divergence for a perturbed trajectory in the direction
of the unperturbed trajectory. The larger the LCE, the greater the rate of exponential divergence and the wider the
corresponding Separatrix of the Chaotic region. For the Standard Map, an analytic estimate of the
width of the Chaotic zone by Chirikov (1979) finds
| (4) |
| (5) |
| (6) |
| (7) |
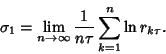 |
(8) |
| (9) |
For Hamiltonian Systems, the LCEs exist in additive inverse pairs, so if ![]() is an LCE, then
so is
is an LCE, then
so is ![]() . One LCE is always 0. For a 1-D oscillator (with a 2-D phase space), the two LCEs therefore must be
. One LCE is always 0. For a 1-D oscillator (with a 2-D phase space), the two LCEs therefore must be
![]() , so the motion is Quasiperiodic and cannot be Chaotic. For
higher order Hamiltonian Systems, there are always at least two 0 LCEs, but other LCEs may enter in
plus-and-minus pairs
, so the motion is Quasiperiodic and cannot be Chaotic. For
higher order Hamiltonian Systems, there are always at least two 0 LCEs, but other LCEs may enter in
plus-and-minus pairs ![]() and
and ![]() . If they, too, are both zero, the motion is integrable and not Chaotic. If
they are Nonzero, the Positive LCE
. If they, too, are both zero, the motion is integrable and not Chaotic. If
they are Nonzero, the Positive LCE ![]() results in an exponential separation of trajectories, which corresponds to a
Chaotic region. Notice that it is not possible to have all LCEs Negative, which explains why convergence of
orbits is never observed in Hamiltonian Systems.
results in an exponential separation of trajectories, which corresponds to a
Chaotic region. Notice that it is not possible to have all LCEs Negative, which explains why convergence of
orbits is never observed in Hamiltonian Systems.
Now consider a dissipative system. For an arbitrary ![]() -D phase space, there must always be one LCE equal to 0, since a perturbation
along the path results in no divergence. The LCEs satisfy
-D phase space, there must always be one LCE equal to 0, since a perturbation
along the path results in no divergence. The LCEs satisfy
![]() . Therefore, for a 2-D phase space of a
dissipative system,
. Therefore, for a 2-D phase space of a
dissipative system,
![]() . For a 3-D phase space, there are three possibilities:
. For a 3-D phase space, there are three possibilities:
See also Chaos, Hamiltonian System, Lyapunov Characteristic Number, Osedelec Theorem
References
Chirikov, B. V. ``A Universal Instability of Many-Dimensional Oscillator Systems.'' Phys. Rep. 52, 264-379, 1979.
|
|
|
© 1996-9 Eric W. Weisstein