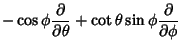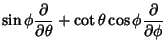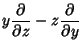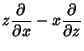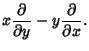If any set of points is displaced by 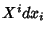 where all distance relationships are unchanged (i.e., there is an
Isometry), then the Vector field is called a Killing vector.
where all distance relationships are unchanged (i.e., there is an
Isometry), then the Vector field is called a Killing vector.
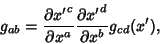 |
(1) |
so let
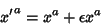 |
(2) |
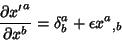 |
(3) |
where 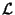 is the Lie Derivative. An ordinary derivative can be replaced with a covariant derivative in a
Lie Derivative, so we can take as the definition
is the Lie Derivative. An ordinary derivative can be replaced with a covariant derivative in a
Lie Derivative, so we can take as the definition
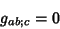 |
(5) |
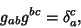 |
(6) |
which gives Killing's Equation
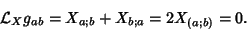 |
(7) |
A Killing vector 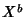 satisfies
satisfies
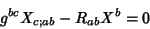 |
(8) |
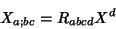 |
(9) |
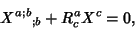 |
(10) |
where 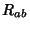 is the Ricci Tensor and
is the Ricci Tensor and 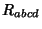 is the Riemann Tensor.
is the Riemann Tensor.
A 2-sphere with Metric
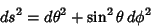 |
(11) |
has three Killing vectors, given by the angular momentum operators 
The Killing vectors in Euclidean 3-space are
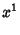 |
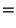 |
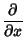 |
(15) |
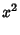 |
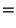 |
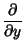 |
(16) |
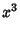 |
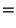 |
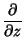 |
(17) |
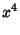 |
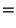 |
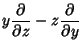 |
(18) |
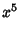 |
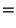 |
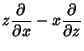 |
(19) |
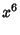 |
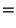 |
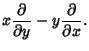 |
(20) |
In Minkowski Space, there are 10 Killing vectors
The first group is Translation, the second Rotation, and the final corresponds to a
``boost  .''
.''
© 1996-9 Eric W. Weisstein
1999-05-26
![]() where all distance relationships are unchanged (i.e., there is an
Isometry), then the Vector field is called a Killing vector.
where all distance relationships are unchanged (i.e., there is an
Isometry), then the Vector field is called a Killing vector.