|
|
|
N.B. A detailed on-line essay by S. Finch was the starting point for this entry.
Let
![\begin{displaymath}
x=[a_0, a_1, \ldots]=a_0+{1\over\strut\displaystyle a_1+{\st...
...2+{\strut\displaystyle 1\over\strut\displaystyle a_3+\ldots}}}
\end{displaymath}](k_421.gif) |
(1) |
| (2) |
| (3) |
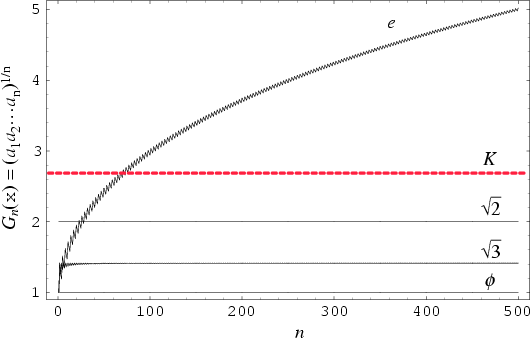
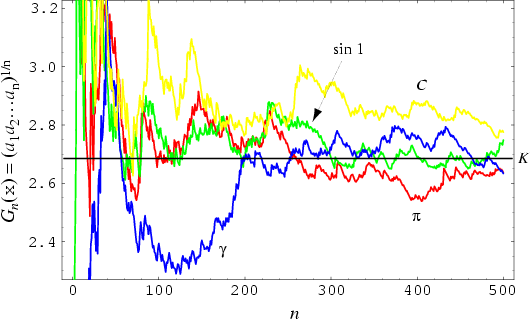
The Continued Fraction for ![]() is [2, 1, 2, 5, 1, 1, 2, 1, 1, ...] (Sloane's A002211). It is not known if
is [2, 1, 2, 5, 1, 1, 2, 1, 1, ...] (Sloane's A002211). It is not known if ![]() is
Irrational, let alone Transcendental. Bailey et al. (1995) have
computed
is
Irrational, let alone Transcendental. Bailey et al. (1995) have
computed ![]() to 7350 Digits.
to 7350 Digits.
Explicit expressions for ![]() include
include
![$\displaystyle \prod_{n=1}^\infty \left[{1+{1\over n(n+2)}}\right]^{\ln n/\ln 2}$](k_436.gif) |
(4) | ||
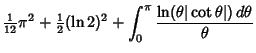 |
(5) | ||
![$\displaystyle {1\over\ln 2}\sum_{m=1}^\infty {h_{m-1}\over m}[\zeta(2m)-1],$](k_440.gif) |
(6) |
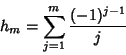 |
(7) |
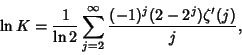 |
(8) |
![$\ln K={1\over\ln 2} \sum_{k=0}^\infty \Biggl\{-\ln(k+1)[\ln(k+3)-2\ln(k+2)+\ln(k+1)]$](k_443.gif)
|
|
|
|
(9) |
Khintchine's constant is also given by the integral
| (10) |
If ![]() is the
is the ![]() th Convergent of the Continued Fraction of
th Convergent of the Continued Fraction of ![]() , then
, then
| (11) |
Define the following quantity in terms of the ![]() th partial quotient
th partial quotient ![]() ,
,
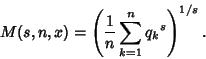 |
(12) |
| (13) |
| (14) |
| (15) |
See also Continued Fraction, Convergent, Khintchine-Lévy Constant, Lévy Constant, Partial Quotient, Simple Continued Fraction
References
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E. ``On the Khintchine Constant.'' Math. Comput. 66, 417-431, 1997.
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/khntchn/khntchn.html
Kac, M. Statistical Independence and Probability, Analysts and Number Theory. Providence, RI: Math. Assoc. Amer., 1959.
Khinchin, A. Ya. Continued Fractions. New York: Dover, 1997.
Knuth, D. E. Exercise 24 in The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd ed.
Reading, MA: Addison-Wesley, p. 604, 1981.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 46, 1983.
Lehmer, D. H. ``Note on an Absolute Constant of Khintchine.'' Amer. Math. Monthly 46, 148-152, 1939.
Phillipp, W. ``Some Metrical Theorems in Number Theory.'' Pacific J. Math. 20, 109-127, 1967.
Plouffe, S. ``Plouffe's Inverter: Table of Current Records for the Computation
of Constants.'' http://www.lacim.uqam.ca/pi/records.html.
Rockett, A. M. and Szüsz, P. Continued Fractions. Singapore: World Scientific, 1992.
Shanks, D. and Wrench, J. W. ``Khintchine's Constant.'' Amer. Math. Monthly 66, 148-152, 1959.
Sloane, N. J. A. Sequences
A002210/M1564
and A002211/M0118
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html and Sloane, N. J. A. and Plouffe, S.
The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.
Vardi, I. ``Khinchin's Constant.'' §8.4 in Computational Recreations in Mathematica.
Reading, MA: Addison-Wesley, pp. 163-171, 1991.
Wrench, J. W. ``Further Evaluation of Khintchine's Constant.'' Math. Comput. 14, 370-371, 1960.
|
|
|
© 1996-9 Eric W. Weisstein