|
|
|
Maximize the distance a jeep can penetrate into the desert using a given quantity of fuel. The jeep is allowed to go forward, unload some fuel, and then return to its base using the fuel remaining in its tank. At its base, it may refuel and set out again. When it reaches fuel it has previously stored, it may then use it to partially fill its tank. This problem is also called the Exploration Problem (Ball and Coxeter 1987).
Given ![]() (with
(with ![]() ) drums of fuel at the edge of the desert and a jeep capable of holding one drum (and storing
fuel in containers along the way), the maximum one-way distance which can be traveled (assuming the jeep travels one unit of
distance per drum of fuel expended) is
) drums of fuel at the edge of the desert and a jeep capable of holding one drum (and storing
fuel in containers along the way), the maximum one-way distance which can be traveled (assuming the jeep travels one unit of
distance per drum of fuel expended) is
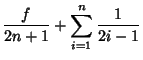 |
|||
![$\displaystyle {f\over 2n+1}+{\textstyle{1\over 2}}[\gamma+2\ln 2+\psi_0({\textstyle{1\over 2}}+n)],$](j_548.gif) |
For example, the farthest a jeep with ![]() drum can travel is obviously 1 unit. However, with
drum can travel is obviously 1 unit. However, with ![]() drums of gas, the
maximum distance is achieved by filling up the jeep's tank with the first drum, traveling 1/3 of a unit, storing 1/3 of a
drum of fuel there, and then returning to base with the remaining 1/3 of a tank. At the base, the tank is filled with the
second drum. The jeep then travels 1/3 of a unit (expending 1/3 of a drum of fuel), refills the tank using the 1/3 of a
drum of fuel stored there, and continues an additional 1 unit of distance on a full tank, giving a total distance of 4/3.
The solutions for
drums of gas, the
maximum distance is achieved by filling up the jeep's tank with the first drum, traveling 1/3 of a unit, storing 1/3 of a
drum of fuel there, and then returning to base with the remaining 1/3 of a tank. At the base, the tank is filled with the
second drum. The jeep then travels 1/3 of a unit (expending 1/3 of a drum of fuel), refills the tank using the 1/3 of a
drum of fuel stored there, and continues an additional 1 unit of distance on a full tank, giving a total distance of 4/3.
The solutions for ![]() , 2, ... drums are 1, 4/3, 23/15, 176/105, 563/315, ..., which
can also be written as
, 2, ... drums are 1, 4/3, 23/15, 176/105, 563/315, ..., which
can also be written as ![]() , where
, where
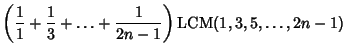 |
|||
See also Harmonic Number
References
Alway, G. C. ``Crossing the Desert.'' Math. Gaz. 41, 209, 1957.
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 32, 1987.
Bellman, R. Exercises 54-55 Dynamic Programming. Princeton, NJ: Princeton University Press, p. 103, 1955.
Fine, N. J. ``The Jeep Problem.'' Amer. Math. Monthly 54, 24-31, 1947.
Gale, D. ``The Jeep Once More or Jeeper by the Dozen.'' Amer. Math. Monthly 77, 493-501, 1970.
Gardner, M. The Second Scientific American Book of Mathematical Puzzles & Diversions: A New Selection.
New York: Simon and Schuster, pp. 152 and 157-159, 1961.
Haurath, A.; Jackson, B.; Mitchem, J.; and Schmeichel, E. ``Gale's Round-Trip Jeep Problem.''
Amer. Math. Monthly 102, 299-309, 1995.
Helmer, O. ``A Problem in Logistics: The Jeep Problem.'' Project Rand Report No. Ra 15015, Dec. 1947.
Phipps, C. G. ``The Jeep Problem, A More General Solution.'' Amer. Math. Monthly 54, 458-462, 1947.
Sloane, N. J. A.
A025550 and
A025547
in ``An On-Line Version of the Encyclopedia of Integer Sequences.''
http://www.research.att.com/~njas/sequences/eisonline.html.
|
|
|
© 1996-9 Eric W. Weisstein