 Integral Equations
Integral Equations
Corduneanu, C. Integral Equations and Applications. Cambridge, England: Cambridge University Press, 1991.
Davis, H. T. Introduction to Nonlinear Differential and Integral Equations. New York: Dover, 1962.
Kondo, J. Integral Equations. Oxford, England: Clarendon Press, 1992.
Lovitt, W. V. Linear Integral Equations. New York: Dover, 1950.
Mikhlin, S. G.
Integral Equations and Their Applications to Certain Problems in Mechanics, Mathematical Physics and Technology, 2nd rev. ed.
New York: Macmillan, 1964.
Mikhlin, S. G. Linear Integral Equations. New York: Gordon & Breach, 1961.
Pipkin, A. C. A Course on Integral Equations. New York: Springer-Verlag, 1991.
Porter, D. and Stirling, D. S. G. Integral Equations: A Practical Treatment, from Spectral Theory to Applications.
Cambridge, England: Cambridge University Press, 1990.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. ``Integral Equations and Inverse Theory.'' Ch. 18
in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 779-817, 1992.
Tricomi, F. G. Integral Equations. New York: Dover, 1957.
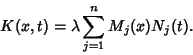
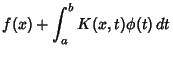
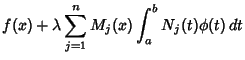
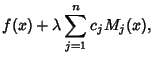
![]() Integral Equations
Integral Equations