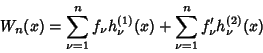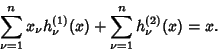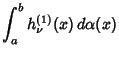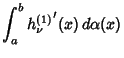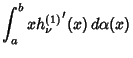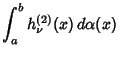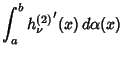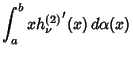Let 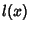 be an
be an 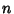 th degree Polynomial with zeros at
th degree Polynomial with zeros at 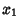 , ...,
, ..., 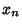 . Then the fundamental
Polynomials are
. Then the fundamental
Polynomials are
![\begin{displaymath}
h^{(1)}_\nu(x)=\left[{1-{l''(x_\nu)\over l'(x_\nu)}}\right][l_\nu(x)]^2
\end{displaymath}](h_1377.gif) |
(1) |
and
![\begin{displaymath}
h^{(2)}_\nu(x)=(x-x_\nu)[l_\nu(x)]^2
\end{displaymath}](h_1378.gif) |
(2) |
for 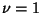 , 2, ...
, 2, ...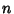 . These polynomials have the properties
. These polynomials have the properties
for 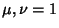 , 2, ...,
, 2, ..., 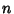 . Now let
. Now let 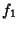 , ...,
, ..., 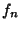 and
and 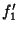 , ...,
, ..., 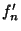 be values. Then the expansion
be values. Then the expansion
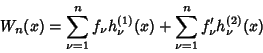 |
(7) |
gives the unique Hermite interpolating fundamental polynomial for which
If 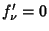 , these are called Step Polynomials. The fundamental polynomials satisfy
, these are called Step Polynomials. The fundamental polynomials satisfy
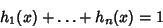 |
(10) |
and
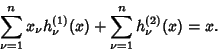 |
(11) |
Also, if 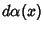 is an arbitrary distribution on the interval
is an arbitrary distribution on the interval ![$[a,b]$](h_1400.gif) , then
, then
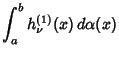 |
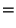 |
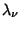 |
(12) |
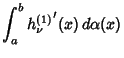 |
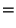 |
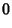 |
(13) |
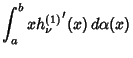 |
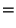 |
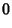 |
(14) |
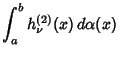 |
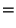 |
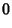 |
(15) |
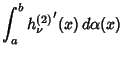 |
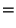 |
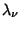 |
(16) |
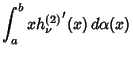 |
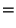 |
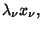 |
(17) |
where 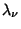 are Christoffel Numbers.
are Christoffel Numbers.
References
Hildebrand, F. B. Introduction to Numerical Analysis. New York: McGraw-Hill, pp. 314-319, 1956.
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., pp. 330-332, 1975.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() be an
be an ![]() th degree Polynomial with zeros at
th degree Polynomial with zeros at ![]() , ...,
, ..., ![]() . Then the fundamental
Polynomials are
. Then the fundamental
Polynomials are