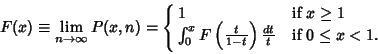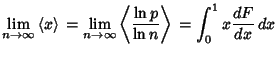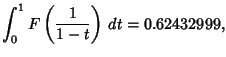N.B. A detailed on-line essay by S. Finch
was the starting point for this entry.
Let  be a Permutation of
be a Permutation of 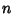 elements, and let
elements, and let 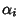 be the number of Cycles of length
be the number of Cycles of length 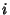 in this Permutation. Picking
in this Permutation. Picking 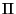 at Random
gives
at Random
gives
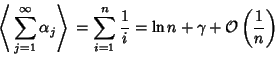 |
(1) |
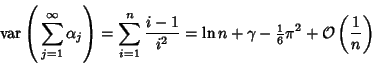 |
(2) |
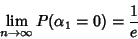 |
(3) |
(Shepp and Lloyd 1966, Wilf 1990). Goncharov (1942) showed that
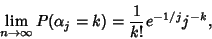 |
(4) |
which is a Poisson Distribution, and
![\begin{displaymath}
\lim_{n\to\infty} P\left[{\left({\,\sum_{j=1}^\infty \alpha_j-\ln n}\right)(\ln n)^{-1/2}\leq x}\right]=\Phi(x),
\end{displaymath}](g_1643.gif) |
(5) |
which is a Normal Distribution, 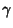 is the Euler-Mascheroni Constant, and
is the Euler-Mascheroni Constant, and 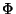 is
the Normal Distribution Function. Let
is
the Normal Distribution Function. Let
Golomb (1959) derived
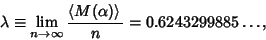 |
(8) |
which is known as the Golomb Constant or Golomb-Dickman constant. Knuth (1981) asked for the constants
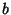 and
and 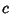 such that
such that
![\begin{displaymath}
\lim_{n\to\infty} n^b[\left\langle{M(\alpha)}\right\rangle{}-\lambda n-{\textstyle{1\over 2}}\lambda]=c,
\end{displaymath}](g_1650.gif) |
(9) |
and Gourdon (1996) showed that
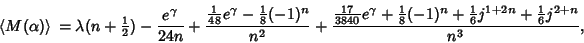 |
(10) |
where
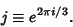 |
(11) |
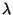 can be expressed in terms of the function
can be expressed in terms of the function 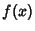 defined by
defined by 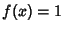 for
for 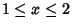 and
and
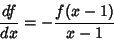 |
(12) |
for 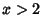 , by
, by
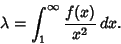 |
(13) |
Shepp and Lloyd (1966) derived
Mitchell (1968) computed 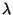 to 53 decimal places.
to 53 decimal places.
Surprisingly enough, there is a connection between 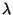 and Prime Factorization (Knuth and Pardo 1976, Knuth 1981, pp. 367-368, 395, and 611). Dickman (1930) investigated the probability
and Prime Factorization (Knuth and Pardo 1976, Knuth 1981, pp. 367-368, 395, and 611). Dickman (1930) investigated the probability
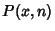 that the largest Prime Factor
that the largest Prime Factor 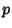 of a random Integer between 1 and
of a random Integer between 1 and 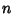 satisfies
satisfies 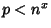 for
for
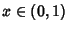 . He found that
. He found that
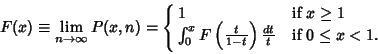 |
(15) |
Dickman then found the average value of 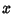 such that
such that 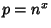 , obtaining
, obtaining
which is 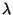 .
.
References
Finch, S. ``Favorite Mathematical Constants.'' http://www.mathsoft.com/asolve/constant/golomb/golomb.html
Gourdon, X. 1996. http://www.mathsoft.com/asolve/constant/golomb/gourdon.html.
Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1973.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1981.
Knuth, D. E. and Pardo, L. T. ``Analysis of a Simple Factorization Algorithm.'' Theor. Comput. Sci. 3, 321-348, 1976.
Mitchell, W. C. ``An Evaluation of Golomb's Constant.'' Math. Comput. 22, 411-415, 1968.
Purdom, P. W. and Williams, J. H. ``Cycle Length in a Random Function.'' Trans. Amer. Math. Soc. 133, 547-551, 1968.
Shepp, L. A. and Lloyd, S. P. ``Ordered Cycle Lengths in Random Permutation.'' Trans. Amer. Math. Soc. 121, 350-557, 1966.
Wilf, H. S. Generatingfunctionology, 2nd ed. New York: Academic Press, 1993.
© 1996-9 Eric W. Weisstein
1999-05-25
![]() be a Permutation of
be a Permutation of ![]() elements, and let
elements, and let ![]() be the number of Cycles of length
be the number of Cycles of length ![]() in this Permutation. Picking
in this Permutation. Picking ![]() at Random
gives
at Random
gives
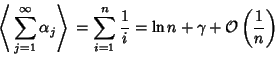
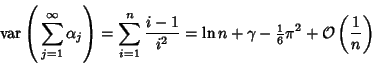
![\begin{displaymath}
\lim_{n\to\infty} P\left[{\left({\,\sum_{j=1}^\infty \alpha_j-\ln n}\right)(\ln n)^{-1/2}\leq x}\right]=\Phi(x),
\end{displaymath}](g_1643.gif)
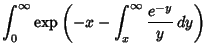
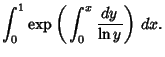
![]() and Prime Factorization (Knuth and Pardo 1976, Knuth 1981, pp. 367-368, 395, and 611). Dickman (1930) investigated the probability
and Prime Factorization (Knuth and Pardo 1976, Knuth 1981, pp. 367-368, 395, and 611). Dickman (1930) investigated the probability
![]() that the largest Prime Factor
that the largest Prime Factor ![]() of a random Integer between 1 and
of a random Integer between 1 and ![]() satisfies
satisfies ![]() for
for
![]() . He found that
. He found that