|
|
|
Gives a region in the Complex Plane containing all the Eigenvalues of a Complex Square Matrix. Let
| (1) |
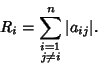 |
(2) |
| (3) |
| (4) |
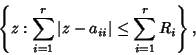 |
(5) |
References
Brualdi, R. A. and Mellendorf, S. ``Regions in the Complex Plane Containing the Eigenvalues of a Matrix.''
Amer. Math. Monthly 101, 975-985, 1994.
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, pp. 1120-1121, 1979.
Taussky-Todd, O. ``A Recurring Theorem on Determinants.'' Amer. Math. Monthly 56, 672-676, 1949.