|
|
|
In a 1631 edition of Academiae Algebrae, J. Faulhaber published the general formula for the Sum of ![]() th
Powers of the first
th
Powers of the first ![]() Positive Integers,
Positive Integers,
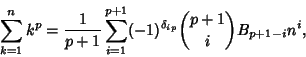 |
(1) |
| (2) | |||
| (3) | |||
| (4) | |||
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
| (10) | |||
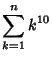 |
(11) |
See also Power, Sum
References
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 106, 1996.