|
|
|
A theorem proved by Doob (1942) which states that any random process which is both Gaussian and Markov has the following forms for its correlation function, spectral density, and probability densities:
| (1) | |||
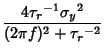 |
(2) | ||
| (3) | |||
![$\displaystyle {1\over \sqrt{2\pi(1-e^{-2\tau/\tau_r}){\sigma_y}^2}}\mathop{\rm ...
...-\tau/\tau_r}(y_1-\bar y)]^2\over 2(1-e^{-2\tau/\tau_r}){\sigma_y}^2}}\right\},$](d2_1473.gif) |
(4) |
References
Doob, J. L. ``Topics in the Theory of Markov Chains.'' Trans. Amer. Math. Soc. 52, 37-64, 1942.