|
|
|
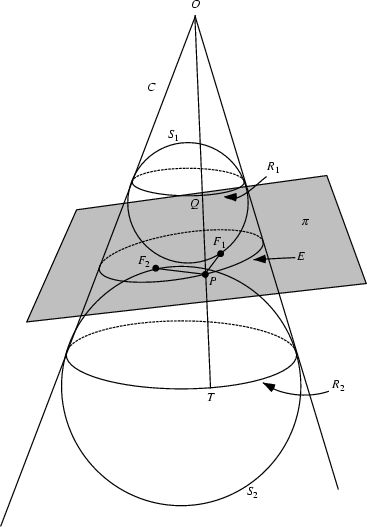
The inner and outer Spheres Tangent internally to a Cone and also to a Plane intersecting the Cone are called Dandelin spheres.
The Spheres can be used to show that the intersection of the Plane with the Cone is an
Ellipse. Let ![]() be a Plane intersecting a right circular Cone with vertex
be a Plane intersecting a right circular Cone with vertex ![]() in the curve
in the curve ![]() .
Call the Spheres Tangent to the Cone and the Plane
.
Call the Spheres Tangent to the Cone and the Plane ![]() and
and ![]() , and the
Circles on which the Spheres are Tangent to the Cone
, and the
Circles on which the Spheres are Tangent to the Cone ![]() and
and ![]() . Pick
a line along the Cone which intersects
. Pick
a line along the Cone which intersects ![]() at
at ![]() ,
, ![]() at
at ![]() , and
, and ![]() at
at ![]() . Call the points on the
Plane where the Circles are Tangent
. Call the points on the
Plane where the Circles are Tangent ![]() and
and ![]() . Because intersecting tangents have the
same length,
. Because intersecting tangents have the
same length,
See also Cone, Sphere
References
Honsberger, R. ``Kepler's Conics.'' Ch. 9 in Mathematical Plums (Ed. R. Honsberger).
Washington, DC: Math. Assoc. Amer., p. 170, 1979.
Honsberger, R. More Mathematical Morsels. Washington, DC: Math. Assoc. Amer., pp. 40-44, 1991.
Ogilvy, C. S. Excursions in Geometry. New York: Dover, pp. 80-81, 1990.
Ogilvy, C. S. Excursions in Mathematics. New York: Dover, pp. 68-69, 1994.