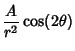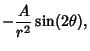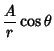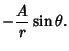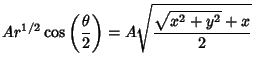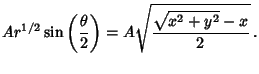By letting 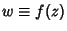 , the Real and Imaginary Parts of
, the Real and Imaginary Parts of 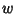 must
satisfy the Cauchy-Riemann Equations and Laplace's Equation, so they automatically provide a scalar
Potential and a so-called stream function.
must
satisfy the Cauchy-Riemann Equations and Laplace's Equation, so they automatically provide a scalar
Potential and a so-called stream function.  If a
physical problem can be found for which the solution is valid, we obtain a solution--which may have been very difficult
to obtain directly--by working backwards. Let
If a
physical problem can be found for which the solution is valid, we obtain a solution--which may have been very difficult
to obtain directly--by working backwards. Let
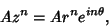 |
(1) |
the Real and Imaginary Parts then give
For 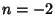 ,
,
which is a double system of Lemniscates (Lamb 1945, p. 69).
For 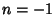 ,
,
This solution consists of two systems of Circles, and 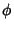 is the Potential Function for two
Parallel opposite charged line charges (Feynman et al. 1989, §7-5; Lamb 1945, p. 69). For
is the Potential Function for two
Parallel opposite charged line charges (Feynman et al. 1989, §7-5; Lamb 1945, p. 69). For 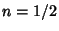 ,
,
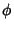 gives the field near the edge of a thin plate (Feynman et al. 1989, §7-5).
For
gives the field near the edge of a thin plate (Feynman et al. 1989, §7-5).
For 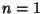 ,
,
This is two straight lines (Lamb 1945, p. 68).
For 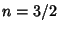 ,
,
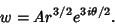 |
(12) |
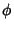 gives the field near the outside of a rectangular corner (Feynman et al. 1989, §7-5).
For
gives the field near the outside of a rectangular corner (Feynman et al. 1989, §7-5).
For 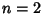 ,
,
![\begin{displaymath}
w=A(x+iy)^2=A[(x^2-y^2)+2ixy]
\end{displaymath}](c2_1169.gif) |
(13) |
These are two Perpendicular Hyperbolas, and 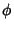 is the Potential Function near the
middle of two point charges or the field on the opening side of a charged Right Angle
conductor
is the Potential Function near the
middle of two point charges or the field on the opening side of a charged Right Angle
conductor  (Feynman 1989, §7-3).
(Feynman 1989, §7-3).
See also Cauchy-Riemann Equations, Conformal Map, Laplace's Equation
References
Feynman, R. P.; Leighton, R. B.; and Sands, M. The Feynman Lectures on Physics, Vol. 1.
Redwood City, CA: Addison-Wesley, 1989.
Lamb, H. Hydrodynamics, 6th ed. New York: Dover, 1945.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() , the Real and Imaginary Parts of
, the Real and Imaginary Parts of ![]() must
satisfy the Cauchy-Riemann Equations and Laplace's Equation, so they automatically provide a scalar
Potential and a so-called stream function.
must
satisfy the Cauchy-Riemann Equations and Laplace's Equation, so they automatically provide a scalar
Potential and a so-called stream function. ![]() If a
physical problem can be found for which the solution is valid, we obtain a solution--which may have been very difficult
to obtain directly--by working backwards. Let
If a
physical problem can be found for which the solution is valid, we obtain a solution--which may have been very difficult
to obtain directly--by working backwards. Let
![]() ,
,