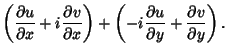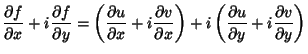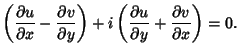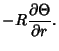Let
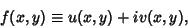 |
(1) |
where
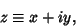 |
(2) |
so
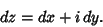 |
(3) |
The total derivative of 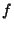 with respect to
with respect to 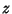 may then be computed as follows.
may then be computed as follows.
so
and
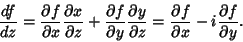 |
(8) |
In terms of 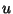 and
and 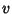 , (8) becomes
, (8) becomes
Along the real, or x-Axis,
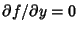 , so
, so
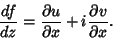 |
(10) |
Along the imaginary, or 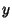 -axis,
-axis,
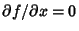 , so
, so
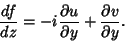 |
(11) |
If 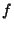 is Complex Differentiable, then the value of the derivative must be the same for a given
is Complex Differentiable, then the value of the derivative must be the same for a given 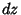 , regardless of its
orientation. Therefore, (10) must equal (11), which requires that
, regardless of its
orientation. Therefore, (10) must equal (11), which requires that
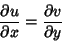 |
(12) |
and
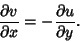 |
(13) |
These are known as the Cauchy-Riemann equations. They lead to the condition
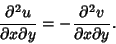 |
(14) |
The Cauchy-Riemann equations may be concisely written as
In Polar Coordinates,
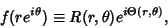 |
(16) |
so the Cauchy-Riemann equations become
If 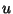 and
and 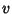 satisfy the Cauchy-Riemann equations, they also satisfy
Laplace's Equation in 2-D, since
satisfy the Cauchy-Riemann equations, they also satisfy
Laplace's Equation in 2-D, since
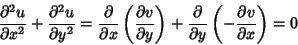 |
(19) |
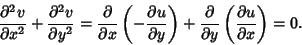 |
(20) |
By picking an arbitrary 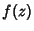 , solutions can be found which automatically satisfy the Cauchy-Riemann equations and
Laplace's Equation. This fact is used to find so-called Conformal Solutions to
physical problems involving scalar potentials such as fluid flow and electrostatics.
, solutions can be found which automatically satisfy the Cauchy-Riemann equations and
Laplace's Equation. This fact is used to find so-called Conformal Solutions to
physical problems involving scalar potentials such as fluid flow and electrostatics.
See also Cauchy Integral Theorem, Conformal Solution, Monogenic Function,
Polygenic Function
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 17, 1972.
Arfken, G. ``Cauchy-Riemann Conditions.'' §6.2 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 3560-365, 1985.
© 1996-9 Eric W. Weisstein
1999-05-26