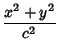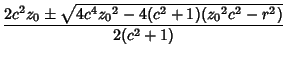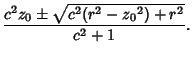Let a Cone of opening parameter 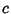 and vertex at
and vertex at 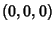 intersect a Sphere of
Radius
intersect a Sphere of
Radius 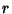 centered at
centered at
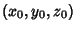 , with the Cone oriented such that its axis does not pass through the
center of the Sphere. Then the equations of the curve of intersection are
, with the Cone oriented such that its axis does not pass through the
center of the Sphere. Then the equations of the curve of intersection are
Combining (1) and (2) gives
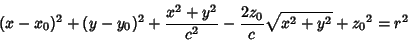 |
(3) |
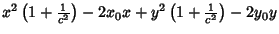
|
|
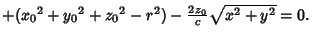
|
(4) |
Therefore, 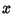 and
and 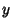 are connected by a complicated Quartic Equation, and
are connected by a complicated Quartic Equation, and 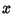 ,
, 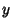 , and
, and 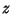 by a Quadratic
Equation.
by a Quadratic
Equation.
If the Cone-Sphere intersection is on-axis so that a Cone of opening parameter 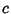 and vertex at
and vertex at
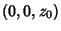 is oriented with its Axis along a radial of the Sphere of radius
is oriented with its Axis along a radial of the Sphere of radius 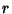 centered at
centered at 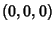 , then
the equations of the curve of intersection are
, then
the equations of the curve of intersection are
Combining (5) and (6) gives
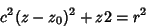 |
(7) |
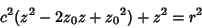 |
(8) |
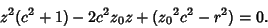 |
(9) |
Using the Quadratic Equation gives
So the curve of intersection is planar. Plugging (10) into (5) shows that the curve is actually a Circle,
with Radius given by
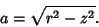 |
(11) |
© 1996-9 Eric W. Weisstein
1999-05-26
![]() and vertex at
and vertex at ![]() intersect a Sphere of
Radius
intersect a Sphere of
Radius ![]() centered at
centered at
![]() , with the Cone oriented such that its axis does not pass through the
center of the Sphere. Then the equations of the curve of intersection are
, with the Cone oriented such that its axis does not pass through the
center of the Sphere. Then the equations of the curve of intersection are
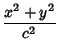
![]() and vertex at
and vertex at
![]() is oriented with its Axis along a radial of the Sphere of radius
is oriented with its Axis along a radial of the Sphere of radius ![]() centered at
centered at ![]() , then
the equations of the curve of intersection are
, then
the equations of the curve of intersection are