|
|
|
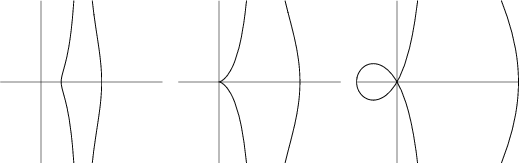
A curve studied by the Greek mathematician Nicomedes in about 200 BC ![]() , also called the Cochloid. It is
the Locus of points a fixed distance away from a line as measured along a line from the Focus point
(MacTutor Archive). Nicomedes recognized the three distinct forms seen in this family. This curve was a favorite with
17th century mathematicians and could be used to solve the problems of Cube Duplication and Angle Trisection.
, also called the Cochloid. It is
the Locus of points a fixed distance away from a line as measured along a line from the Focus point
(MacTutor Archive). Nicomedes recognized the three distinct forms seen in this family. This curve was a favorite with
17th century mathematicians and could be used to solve the problems of Cube Duplication and Angle Trisection.
| (1) |
| (2) |
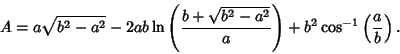 |
(3) |
See also Conchoid
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 135-139, 1972.
Lee, X. ``Conchoid of Nicomedes.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/ConchoidOfNicomedes_dir/conchoidOfNicomedes.html.
MacTutor History of Mathematics Archive. ``Conchoid.''
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Conchoid.html.
Pappas, T. ``Conchoid of Nicomedes.'' The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, pp. 94-95, 1989.
Yates, R. C. ``Conchoid.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 31-33, 1952.