|
|
|
A curve whose name means ``shell form.'' Let ![]() be a curve and
be a curve and ![]() a fixed point. Let
a fixed point. Let ![]() and
and ![]() be points on a line
from
be points on a line
from ![]() to
to ![]() meeting it at
meeting it at ![]() , where
, where ![]() , with
, with ![]() a given constant. For example, if
a given constant. For example, if ![]() is a
Circle and
is a
Circle and ![]() is on
is on ![]() , then the conchoid is a Limaçon, while in the special case that
, then the conchoid is a Limaçon, while in the special case that ![]() is the Diameter of
is the Diameter of ![]() , then the conchoid is a Cardioid. The equation for a parametrically represented
curve
, then the conchoid is a Cardioid. The equation for a parametrically represented
curve ![]() with
with ![]() is
is
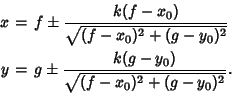
See also Concho-Spiral, Conchoid of de Sluze, Conchoid of Nicomedes, Conical Spiral, Dürer's Conchoid
References
Lawrence, J. D. A Catalog of Special Plane Curves. New York: Dover, pp. 49-51, 1972.
Lee, X. ``Conchoid.''
http://www.best.com/~xah/SpecialPlaneCurves_dir/Conchoid_dir/conchoid.html.
Lockwood, E. H. ``Conchoids.'' Ch. 14 in A Book of Curves. Cambridge, England: Cambridge University Press,
pp. 126-129, 1967.
Yates, R. C. ``Conchoid.'' A Handbook on Curves and Their Properties. Ann Arbor, MI: J. W. Edwards, pp. 31-33, 1952.