|
|
|
The central difference for a function tabulated at equal intervals ![]() is defined by
is defined by
| (1) |
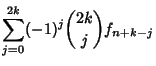 |
(2) | ||
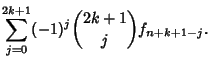 |
(3) |
See also Backward Difference, Divided Difference, Forward Difference
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Differences.'' §25.1 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 877-878, 1972.