|
|
|
The backward difference is a Finite Difference defined by
| (1) |
| (2) | |||
| (3) |
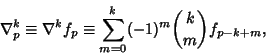 |
(4) |
Newton's Backward Difference Formula expresses ![]() as the sum of the
as the sum of the ![]() th backward differences
th backward differences
| (5) |
See also Adams' Method, Difference Equation, Divided Difference, Finite Difference, Forward Difference, Newton's Backward Difference Formula, Reciprocal Difference
References
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press,
pp. 429 and 433, 1987.