|
|
|
Adams' method is a numerical Method for solving linear First-Order Ordinary Differential Equations of the form
| (1) |
| (2) |
| (3) |
| (4) |
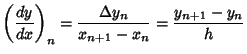 |
(5) | ||
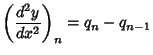 |
(6) | ||
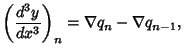 |
(7) |
For first-order interpolation, the method proceeds by iterating the expression
| (8) |
| (9) |
|
|
|
|
|
(10) |
See also Gill's Method, Milne's Method, Predictor-Corrector Methods, Runge-Kutta Method
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, p. 896, 1972.
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 455, 1987.
Kármán, T. von and Biot, M. A. Mathematical Methods in Engineering: An Introduction to the
Mathematical Treatment of Engineering Problems. New York: McGraw-Hill, pp. 14-20, 1940.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge
University Press, p. 741, 1992.
|
|
|
© 1996-9 Eric W. Weisstein