|
|
|
The divided difference
![]() on
on ![]() points
points ![]() ,
, ![]() , ...,
, ..., ![]() of a function
of a function ![]() is
defined by
is
defined by
![]() and
and
| (1) |
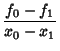 |
(2) | ||
![$\displaystyle {[x_0, x_1]-[x_1, x_2]\over x_0-x_2}$](d2_1137.gif) |
(3) | ||
![$\displaystyle {[x_0, \ldots, x_{n-1}]-[x_1, \ldots, x_n]\over x_0-x_n}.$](d2_1139.gif) |
(4) |
| (5) |
| (6) |
![\begin{displaymath}[x_0, x_1, \ldots, x_n]=\sum_{k=0}^n {f_k\over \pi_n'(x_k)}.
\end{displaymath}](d2_1142.gif) |
(7) |
Consider the following question: does the property
| (8) |
See also Newton's Divided Difference Interpolation Formula, Reciprocal Difference
References
Abramowitz, M. and Stegun, C. A. (Eds.).
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 877-878, 1972.
Aczél, J. ``A Mean Value Property of the Derivative of Quadratic Polynomials--Without Mean Values and
Derivatives.'' Math. Mag. 58, 42-45, 1985.
Andersen, K. M. ``A Characterization of Polynomials.'' Math. Mag. 69, 137-142, 1996.
Bailey, D. F. ``A Mean-Value Property of Cubic Polynomials--Without Mean Values.'' Math. Mag. 65, 123-124, 1992.
Beyer, W. H. (Ed.) CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 439-440, 1987.
Schwaiger, J. ``On a Characterization of Polynomials by Divided Differences.'' Aequationes Math. 48, 317-323, 1994.
|
|
|
© 1996-9 Eric W. Weisstein