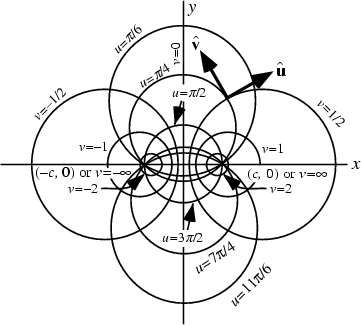
A set of Curvilinear Coordinates defined by
where
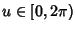 ,
,
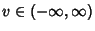 , and
, and
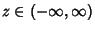 . There are several notational conventions,
and whereas
. There are several notational conventions,
and whereas 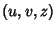 is used in this work, Arfken (1970) prefers
is used in this work, Arfken (1970) prefers
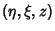 . The following identities show that curves
of constant
. The following identities show that curves
of constant 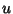 and
and 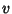 are Circles in
are Circles in 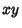 -space.
-space.
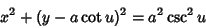 |
(4) |
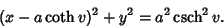 |
(5) |
The Scale Factors are
The Laplacian is
Laplace's Equation is not separable in Bipolar Cylindrical Coordinates, but it is in 2-D Bipolar Coordinates.
References
Arfken, G. ``Bipolar Coordinates (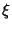 ,
, 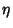 ,
, 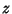 ).'' §2.9 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 97-102, 1970.
).'' §2.9 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 97-102, 1970.
© 1996-9 Eric W. Weisstein
1999-05-26
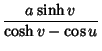
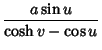
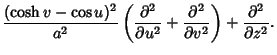
![]() ,
, ![]() ,
, ![]() ).'' §2.9 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 97-102, 1970.
).'' §2.9 in
Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 97-102, 1970.