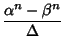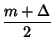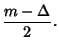The two Recurrence Sequences
with 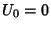 ,
, 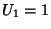 and
and 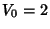 ,
, 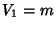 , can be solved for the individual
, can be solved for the individual 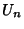 and
and 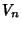 . They are given by
. They are given by
where
A useful related identity is
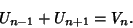 |
(8) |
Binet's Formula is a special case of the Binet form for 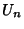 corresponding to
corresponding to 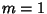 .
.
See also Fibonacci Q-Matrix
© 1996-9 Eric W. Weisstein
1999-05-26