A special case of the 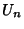 Binet Form with
Binet Form with 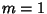 , corresponding to the
, corresponding to the 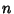 th Fibonacci
Number,
th Fibonacci
Number,
It was derived by Binet in 1843, although the result was known to Euler  and to
Daniel Bernoulli
and to
Daniel Bernoulli  more than a century earlier.
more than a century earlier.
See also Binet Forms, Fibonacci Number
© 1996-9 Eric W. Weisstein
1999-05-26
![]() Binet Form with
Binet Form with ![]() , corresponding to the
, corresponding to the ![]() th Fibonacci
Number,
th Fibonacci
Number,